0
1600
3200
4800
6400 Jahre
N0
N0 / 2
N0 / 4
N0 / 8

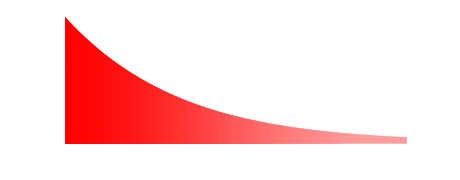
Zerfallsereignisse

0

Atome Ra 226

Jahre Anzahl
0
1600
3200
4800
6400
Loading

Halbwertszeit und Alpha-Zerfall

Medieninfo
Aufgabe
Die Simulation veranschaulicht modellhaft den α-Zerfall von Radium 226 mit einer Halbwertszeit von 1600 Jahren.
In Diagramm und Tabelle wird die Anzahl der vorhandenen Kerne bzw. Zerfallsereignisse ausgehend von der Menge N0 in Relation zur Zeit gesetzt. Die Anzahl radioaktiver Zerfälle lässt sich mit Messgeräten bestimmen. Sie halbiert sich in für jedes radioaktive Isotop charakteristischen, konstanten Zeitabschnitten.
Unter der Halbwertszeit (T1/2) eines radioaktiven Isotopes versteht man also die Zeitspanne, in der die Zahl der Kernumwandlungen auf den halben Wert zurückgeht.
Ihr Betrag reicht von Sekundenbruchteilen bis hin zu Milliarden Jahren. Genau genommen ist sie ein Mittelwert aus den Zerfällen einer großen Zahl von Kernen, also sehr vielen Zerfällen eines Isotopes. Der Zerfall einzelner Kerne ist nicht vorhersagbar.

Optionen

Ernst Klett GmbH, Stuttgart

© Ernst Klett Verlag GmbH
Rotebühlstraße 77
70178 Stuttgart 2014
Alle Rechte vorbehalten
www.klett.de

Das Werk und seine Teile sind urheberrechtlich geschützt. Das gleiche gilt für das Programm sowie das Begleitmatenal. Jede Nutzung in anderen als den gesetzlich zugelassenen Fällen
bedarf der vorherigen schriftlichen Einwilligung des Verlages.

Hinweis zu § 52 a UrhG: Weder das Werk noch seine Teile dürfen ohne eine solche Einwilligung überspielt, gespeichert und in ein Netzwerk eingestellt werden. Dies gilt auch für Intranets von Schulen und sonstigen Bildungseinrichtungen.

Ansprechpartner
Michael Wagner

Naturwissenschaftliche Medienmodule, Autoren:
Prof. Dr. Bernd Baumann, Wolfram Bäurle, Joachim Böttner
Maria Beier, Dr. Irmtraud Beyer, Manfred Bergau
Prof. Dr. Susanne Bickel-Sandkötter, Dr. Angelika Gauß
Paul Gietz, Carola Gorke, Barbara Hoppe, Dr. Jürgen Kirstein
et al., Andrea Kunz, Prof. Dr. Horst Müller, Prof. Dr. Peter Möller
Reinhard Peppmeier, Dr. Helmut Prechtl, Burkhard Priesnitz
Sonja Riedel, Hans Joachim Rösner, Bernd Schäpers
Burkhard Schäfer, Karola Schnurr, Thomas Seilnacht
Dr. Hans-Jürgen Seitz, Bernhard Spieldenner, Gregor Svoboda
Karl-Heinz Umlauft, Heiko Wontroba, Martina Weißmeyer
Dr. Norbert Welsch et al., Welsch & Partner,Jörg Wolter

Softwareentwicklung und Screendesign
Welsch & Partner, Tübingen

Naturwissenschaftliche Medienmodule, Animationen, Grafiken:
Mathias Balonier, Lützelbach
DIM Digitale Medien, Berlin
iAS interActive Systems GmbH, Marburg
Dr. Jürgen Kirstein et al, TU Berlin Jörg Mair, Herrsching
Karin Mall, Berlin Alfred Marzell, Schwäbisch Gmünd
normaldesign GbR (Maria und Jens-Peter Becker), s.u. PSE
Bernhard Spieledenner, Schwalbach/Saar
Welsch & Partner, Tübingen
Prof. Jürgen Wirth, Dreieich

Grafiken PSE
normaldesign GbR (Maria und Jens-Peter Becker),
Schwäbisch Gmünd