Mit einem Mikroskop kann man starke Vergrößerungen (bis zu 1600fach) erzielen und somit sehr kleine Gegenstände betrachten.
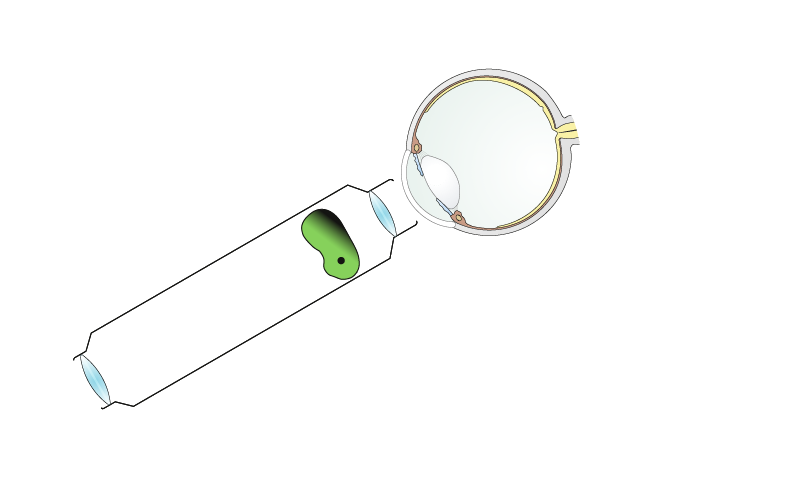
Das Mikroskop besteht aus mindestens zwei Sammellinsen, eine im Objektiv und die andere im Okular.




Die Objektivlinse hat eine sehr kleine Brennweite (wenige Millimeter), damit man sie nahe an den zu betrachtenden Gegenstand bringen kann.
Man stellt den Abstand der Objektivlinse zum Gegenstand so ein, dass er nur geringfügig größer als die Brennweite der Objektivlinse ist.
Man stellt den Abstand der Objektivlinse zum Gegenstand so ein, dass er nur geringfügig größer als die Brennweite der Objektivlinse ist.
g ≈ fobj





bobj
BZ
Die Objektivlinse erzeugt dann ein vergrößertes Zwischenbild BZ des Gegenstandes.
fObj


fOku
bobj
fObj
Dieses Zwischenbild wird nun mit der Okularlinse als Lupe betrachtet.

B0
BM
Die Vergrößerung ist definiert als
Dabei ist BM die Bildgröße im Auge beim Betrachten des
Gegenstandes mit Mikroskop und B0 die Bildgröße ohne Mikroskop
beim Betrachten des Gegenstandes in deutlicher Sehweite.
| VM | = |
|


B0
g0
b0
Nach dem Abbildungsgesetz ist
Dabei ist b0 die Bildweite im Auge, d. h. der Abstand von der
Augenlinse zur Netzhaut, und g0 = 25 cm (deutliche Sehweite).
| = |
| ⇔ | B0 | = |
|


B0
g0
b0
bobj
g ≈ fobj
G
BZ
Ebenso erhält man für das vom Objektiv erzeugte Zwischenbild
Da man beim Mikroskop g = fObj setzen kann.
| = |
| ⇔ | BZ | = |
|






BL = BM
fOku
b0
BZ
BZ
Dieses Zwischenbild ist nun der Gegenstand, der mit dem Okular als Lupe betrachtet wird. Für die Lupe gilt
BL ist aber gerade die gesuchte Bildgröße BM
| = |
| ⇔ | BL | = |
|
Setzt man nun die Gleichungen
in die Gleichung für die Vergrößerung beim Mikroskop ein, erhält man schließlich
Die Vergrößerung VM des Mikroskopes ist das Produkt aus Objektivvergrößerung VObj und Okularvergrößerung VOku.
| B0 | = |
|
| BZ | = |
|
|
| BM | = |
|
in die Gleichung für die Vergrößerung beim Mikroskop ein, erhält man schließlich
| VM | = |
|
= |
| = |
|
· |
| = | VObj | · | VOku |
Die Vergrößerung VM des Mikroskopes ist das Produkt aus Objektivvergrößerung VObj und Okularvergrößerung VOku.

