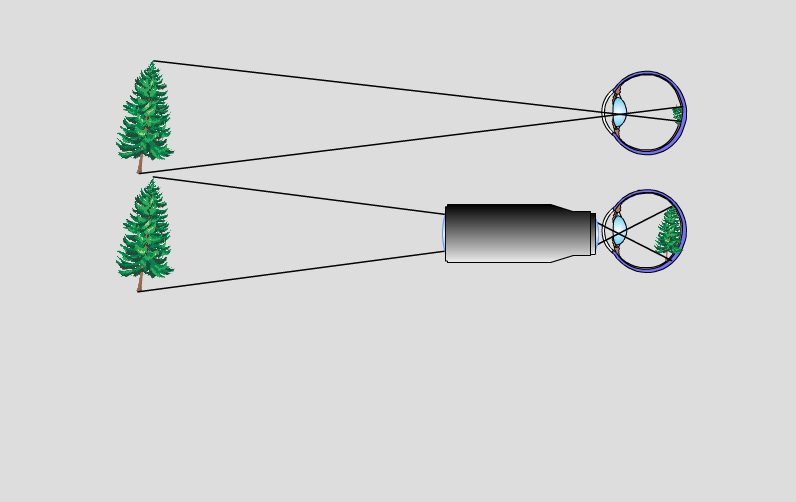
Mit einem Fernrohr kann man weit entfernte Gegenstände vergrößert betrachten.
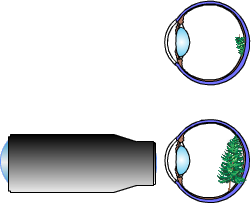


Objektiv
Zwischenbild
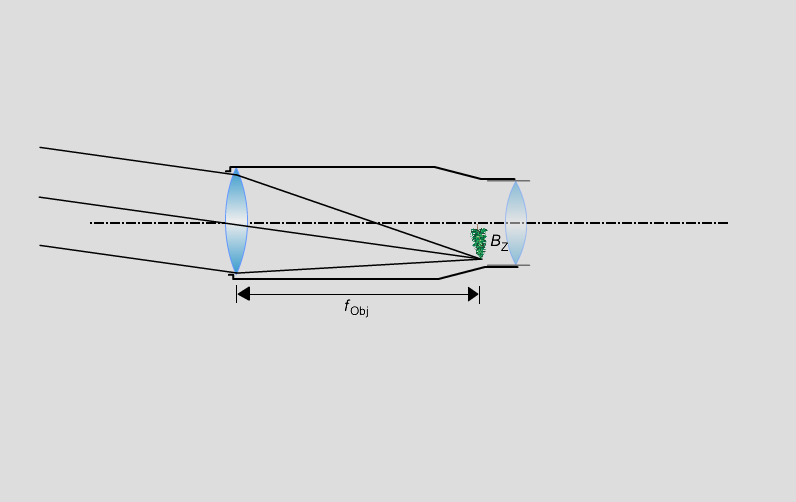
Wie beim Mikroskop wird zunächst mit einer Sammellinse als Objektiv ein Zwischenbild erzeugt. Weil die Gegenstandsweite sehr groß ist, ist dieses Zwischenbild - anders als beim Mikroskop - kleiner als der Gegenstand.
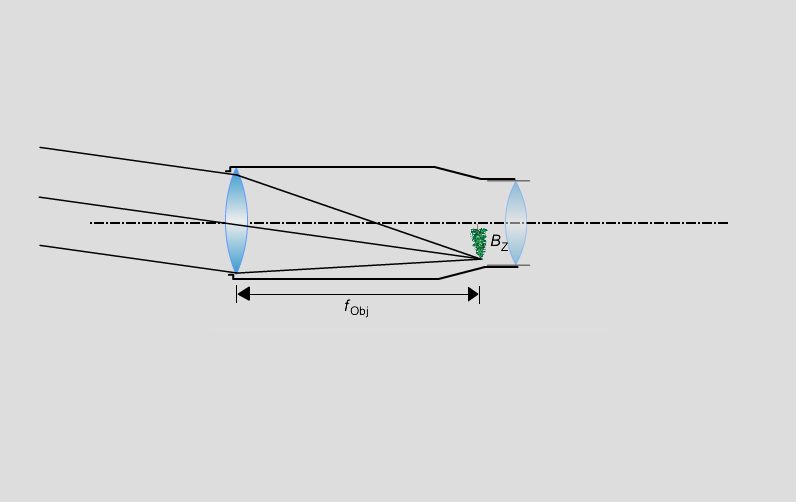

Okular
Objektiv
Zwischenbild
Das Objektiv hat beim Fernrohr die Aufgabe, ein reelles Bild des Gegenstandes in die Nähe des Betrachters zu bringen. Es wird dann - wie beim Mikroskop - mit dem Okular als Lupe betrachtet.
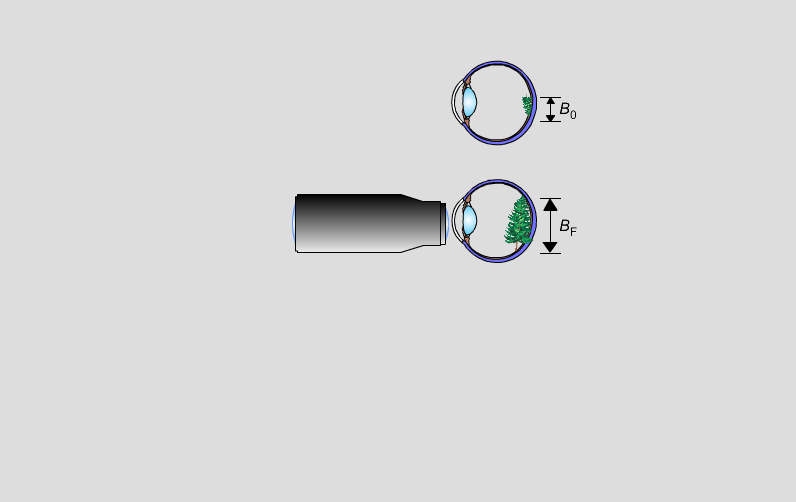
Die Vergrößerung ist definiert als
Dabei ist BF die Bildgröße im Auge beim Betrachten mit Fernrohr und B0 die Bildgröße ohne Fernrohr. Im Unterschied zum Mikroskop ist beim Fernrohr die Bildgröße BF kleiner als die Gegenstandsgröße G.
| VF | = |
|
Dabei ist BF die Bildgröße im Auge beim Betrachten mit Fernrohr und B0 die Bildgröße ohne Fernrohr. Im Unterschied zum Mikroskop ist beim Fernrohr die Bildgröße BF kleiner als die Gegenstandsgröße G.
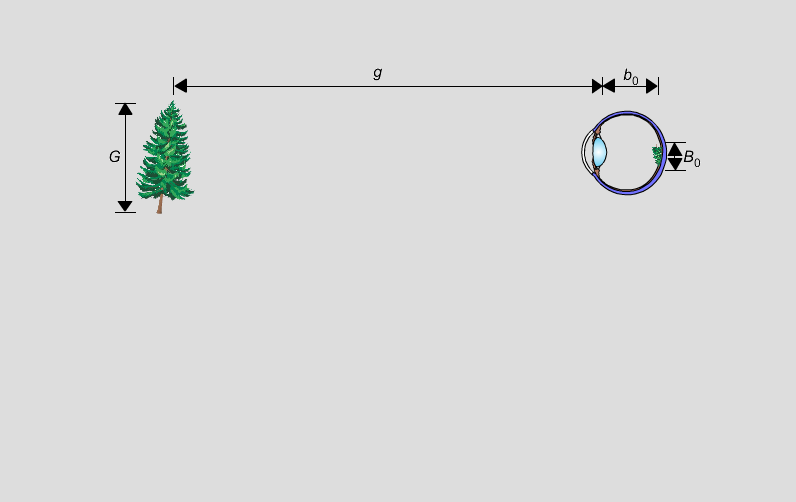
Nach dem Abbildungsgesetz ist
Dabei ist b0 die Bildweite im Auge, d. h. der Abstand von der Augenlinse zur Netzhaut.
| = |
| ⇔ | B0 | = |
|
Dabei ist b0 die Bildweite im Auge, d. h. der Abstand von der Augenlinse zur Netzhaut.
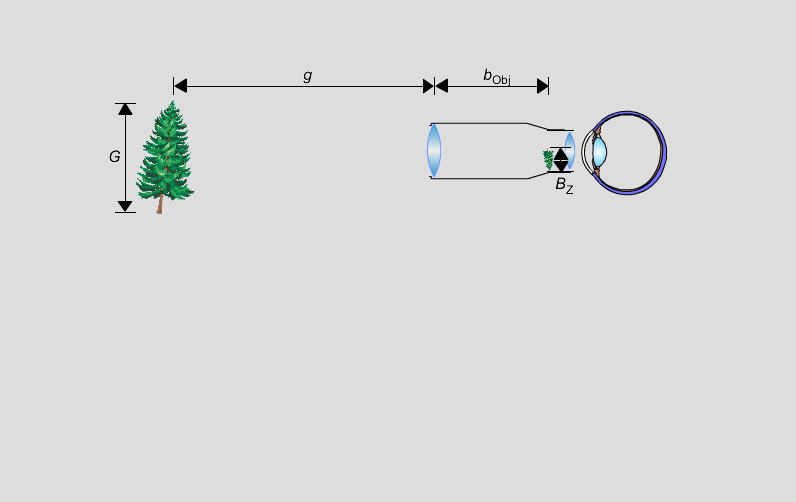
Ebenso erhält man für das vom Objektiv erzeugte Zwischenbild
| = |
| ⇔ | BZ | = |
|
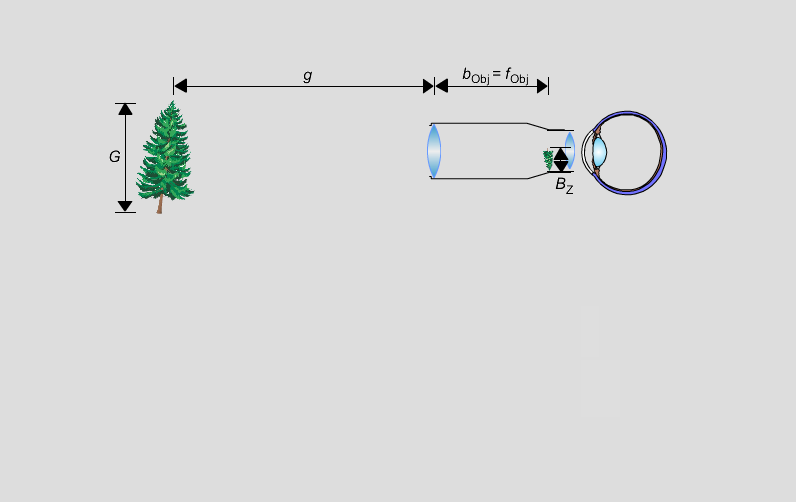
Da die Gegenstandsweite sehr groß ist, ist die Bildweite
ungefähr gleich der Brennweite des Objektivs, d. h., man
kann
bObj = fObj setzen. Damit ist dann
bObj = fObj setzen. Damit ist dann
| BZ | = |
|
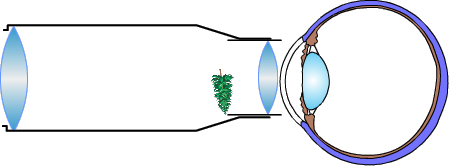


Dieses Zwischenbild ist nun der Gegenstand, der mit dem
Okular als Lupe betrachtet wird. Für die Lupe gilt:
BL ist aber gerade die gesuchte Bildgröße BF.
| = |
| ⇔ | BL | = |
|
BL ist aber gerade die gesuchte Bildgröße BF.

Da die Gegenstandsweite sehr groß ist, ist die Bildweite
ungefähr gleich der Brennweite des Objektivs, d. h., man
kann
bObj = fObj setzen. Damit ist dann
bObj = fObj setzen. Damit ist dann
Setzt man nun die Gleichungen
in die Gleichung für die Vergrößerung beim Fernrohr ein, erhält man schließlich
Die Vergrößerung VF des Fernrohres ist proportional zur Brennweite des Objektivs und umgekehrt proportional zur Brennweite des Okulars.
| B0 | = |
|
| BZ | = |
|
|
| BF | = |
|
in die Gleichung für die Vergrößerung beim Fernrohr ein, erhält man schließlich
| VF | = |
| = |
|
Die Vergrößerung VF des Fernrohres ist proportional zur Brennweite des Objektivs und umgekehrt proportional zur Brennweite des Okulars.

